Another square root clipping

This time from Paul Hsieh

---

Begin quoted text

---

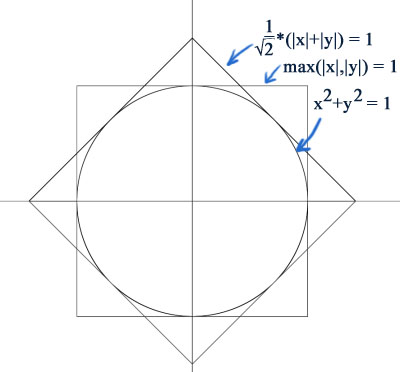
A common application in computer graphics, is to work out the distance between two points as √(Δx²+Δy²). However, for performance reasons, the square root operation is a killer, and often, very crude approximations are acceptable. So we examine the metrics (1 / √2)*(|x|+|y|), and max(|x|,|y|):

Notice the octagonal intersection of the area covered by these metrics, that very tightly fits around the ordinary distance metric. The metric that corresponds to this, therefore is simply:

        octagon(x,y) = min ((1 / √2)*(|x|+|y|), max (|x|, |y|))

With a little more work we can bound the distance metric between the following pair of octagonal metrics:

        octagon(x,y) / (4-2*√2) ≤ √(x²+y²) ≤ octagon(x,y)

Where 1/(4-2*√2) ≈ 0.8536, which is not that far from 1. So we can get a crude approximation of the distance metric without a square root with the formula:

        distanceapprox (x, y) = (1 + 1/(4-2*√2))/2 * min((1 / √2)*(|x|+|y|), max (|x|, |y|))

which will deviate from the true answer by at most about 8%. A similar derivation for 3 dimensions leads to:

        distanceapprox (x, y, z) = (1 + 1/⁴√3)/2 * min((1 / √3)*(|x|+|y|+|z|), max (|x|, |y|, |z|))

with a maximum error of about 16%.

However, something that should be pointed out, is that often the distance is only required for comparison purposes. For example, in the classical mandelbrot set (z←z²+c) calculation, the magnitude of a complex number is typically compared to a boundary radius length of 2. In these cases, one can simply drop the square root, by essentially squaring both sides of the comparison (since distances are always non-negative). That is to say:

        √(Δx²+Δy²) < d is equivalent to Δx²+Δy² < d², if d ≥ 0

---

End quoted text

---

Reference: http://www.azillionmonkeys.com/qed/sqroot.html

CORDIC overview

Description

http://opencores.org/project,cordic

As the name suggests the CORDIC algorithm was developed for rotating coordinates, a piece of hardware for doing real-time navigational computations in the 1950's. The CORDIC uses a sequence like successive approximation to reach its results. The nice part is it does this by adding/subtracting and shifting only. Suppose we want to rotate a point(X,Y) by an angle(Z). The coordinates for the new point(X_new, Y_new) are:

X_new = X * cos(Z) - Y * sin(Z)
Y_new = Y * cos(Z) + X * sin(Z)

Or rewritten:

X_new / cos(Z) = X - Y * tan(Z)
Y_new / cos(Z) = Y + X * tan(Z)

It is possible to break the angle into small pieces, such that the tangents of these pieces are always a power of 2. This results in the following equations:

X(n+1) = P(n) * ( X(n) - Y(n) / 2^n) Y(n+1) = P(n) * ( Y(n) + X(n) / 2^n) Z(n) = atan(1/2^n)

The atan(1/2^n) has to be pre-computed, because the algorithm uses it to approximate the angle. The P(n) factor can be eliminated from the equations by pre-computing its final result. If we multiply all P(n)'s together we get the aggregate constant.

P = cos(atan(1/2^0)) * cos(atan(1/2^1)) * cos(atan(1/2^2))....cos(atan(1/2^n))

This is a constant which reaches 0.607... Depending on the number of iterations and the number of bits used. The final equations look like this:

Xnew = 0.607... * sum( X(n) - Y(n) / 2^n) Ynew = 0.607... * sum( Y(n) + X(n) / 2^n)

Now it is clear how we can simply implement this algorithm, it only uses shifts and adds/subs. Or in a program-like style:

for i=0 to n-1
  if (Z(n) >= 0) then
    X(n + 1) := X(n) – (Yn/2^n);
    Y(n + 1) := Y(n) + (Xn/2^n);
    Z(n + 1) := Z(n) – atan(1/2^i);
  else
    X(n + 1) := X(n) + (Yn/2^n);
    Y(n + 1) := Y(n) – (Xn/2^n);
    Z(n + 1) := Z(n) + atan(1/2^i);
  end if;
end for;

Where 'n' represents the number of iterations.

CORDIC implementations in hardware

• A sine computer in MyHDL (a Python-based HDL)
. CORDIC is used within the sine computer.
• A survey of CORDIC algorithms for FPGA based computers (PDF), by Ray Andraka, presented in FPGA 98.
• A very good tutorial overview of CORDIC PDF: CORDIC for Dummies
• Project report PDF of Verilog implementation by two students in George Mason University
  

Removing unneeded Ubuntu kernels

The command line way:

sudo apt-get remove --purge 2.6.2x-xx-*

where x is the old kernel version subversion numbers. Before that you need to give

uname -r

to find the current version and dont remove that.

JPEG Compression Source Code

• a smaller jpg encoder
• JPEGsnoop source code - useful software for reporting many stats inside JPEG files